\(\Im\)
Imagine that you are invited to a party, and there is a special rule: as the host intends to facilitate socialization and enliven the event, every pair of previously unacquainted persons must sing karaoke together for 2 minutes. However, you also have an appointment 2 hours after the party starts. You know there are 15 people at the party, and since the host also doesn't want to listen to too many overconfident singers, they assure you that for any group of 4 people, there is at least one pair of acquaintances. Now, would you be able to listen to all karaoke performances before you leave for the appointment (assuming as soon as one karaoke performance ends, the next one starts, until the end of the party)?
Or suppose you are the host of a party, and now you have to distribute your guests to different (possibly one) table(s). Each table is round and large, and once seated, every person is surrounded by two other people. Before the party, you were given the complete list of friendships among the guests. Now, do you know whether it's possible to allocate everyone to some table such that both the people surrounding them are their friends?

If you are tired of parties, how about the following: in Königsberg (now known as Kaliningrad in Russia), there were seven bridges connecting some lands and islands as shown below:
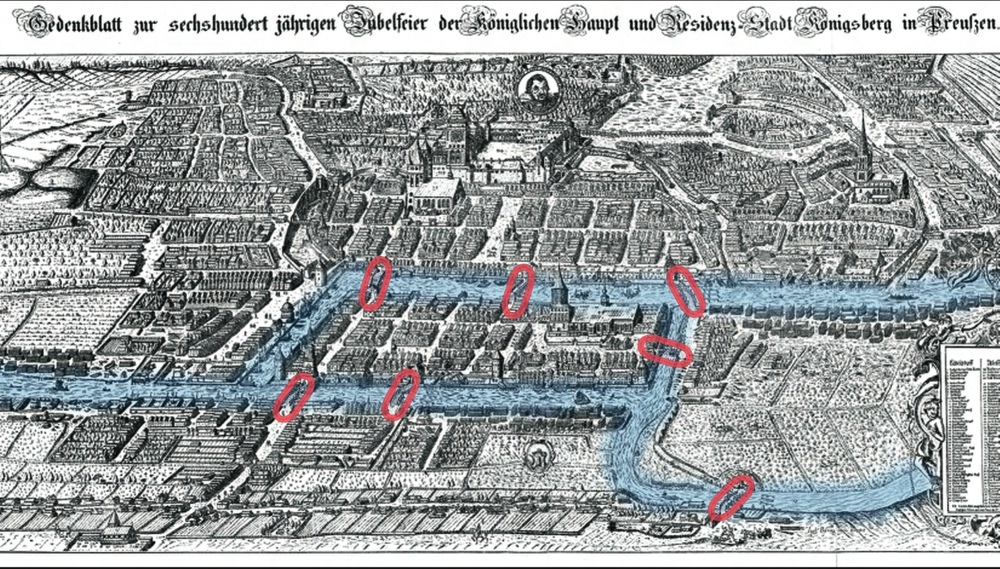
Is it possible to start somewhere in this map and walk around, using every bridge once, and eventually return to the starting location without repeating any bridge? More interestingly, the configuration of the bridges nowadays is different from before due to the bombing of Königsberg during World War II:
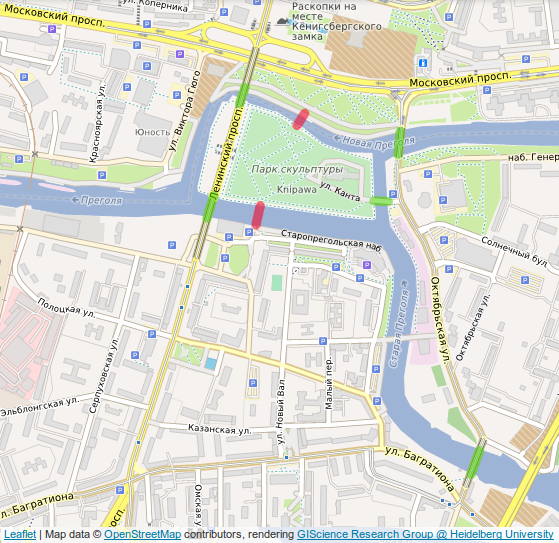
The red marks indicate the destroyed bridges, and the green ones are preserved. How about now?
\(\Im\)
In fact, all of these questions can be answered using a powerful tool in combinatorics, namely graph theory. Let's explore it from the very basic level and appreciate its ubiquitous wonder.
start exploring...