WW Glossary

Note: all definitions are assumed to be in the context of undirected graphs unless specified otherwise.

def

Graph: a diagram constituted by points (vertices) and some (possibly no) lines (edges) that connects some pairs of those points. It may be viewed as a visualization of the relationships between various components in a network.

def's

The number of vertices of a graph $G$ is the order of $G$, and the number of edges of $G$ is the size of $G$.

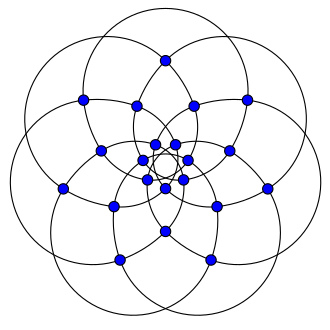
Note: A graph can be described as $G=(V, E)$, where $V$ is the set of vertices and $E$ is the set of edges in $G$.

The embedment below is interactive: left-click to create a vertex; drag from a vertex to another vertex to create an edge; right-click to delete.

def

The number of edges connected to a vertex $v$ is the degree of $v$, denoted as $deg(v)$.

For example, every vertex of the graph in the image above has degree 4.

def

If a graph $G$ has no loops (edges starting and ending at the same vertex) and no multiple edges between the same pair of points, then $G$ is simple.

def

If a sequence of distinct edges $e_1e_2...e_k$ is such that one can walk continuously through them, then it's a trail.

Note: an edge can also be expressed in terms of the vertices it connects (e.g $v_1v_2$ is the edge that connects vertices $v_1$ and $v_2$).

def

A walk is similar to a trail, except all edges walked through need not to be distinct.

The embedment below is interactive: click an edge to indicate a part of a trail. A green border indicates the most recent vertex passed by a walk. Note: this embedment doesn't allow repeated edges.

def

A trail that doesn't touch any vertex twice is a path.

def

A trail using all edges of $G$ is an Eulerian trail of $G$.

def

A trail that ends at the starting vertex is a closed trail.

def

A closed trail that doesn't touch any vertex twice is a cycle.

def

A cycle or path including all vertices of $G$ is a Hamiltonian cycle or Hamiltonian path of $G$.

def's

A graph with an empty edge set is an empty graph. A graph with an empty vertex set and an empty edge set is a null graph. A graph with a singleton vertex set and an empty edge set is a trivial graph.

def

If $ab$ ($a$, $b$ are vertices) is an edge in a graph, then $a$ and $b$ are adjacent. Similarly, two edges are adjacent if they are incident on the same vertex.

def

Let $G=(V(G), E(G)), H=(V(H), E(H)).$ If $V(H) \subseteq V(G)$ and $E(H) \subseteq E(G)$, then $H$ is a subgraph of $G$, or $H \subseteq G$.

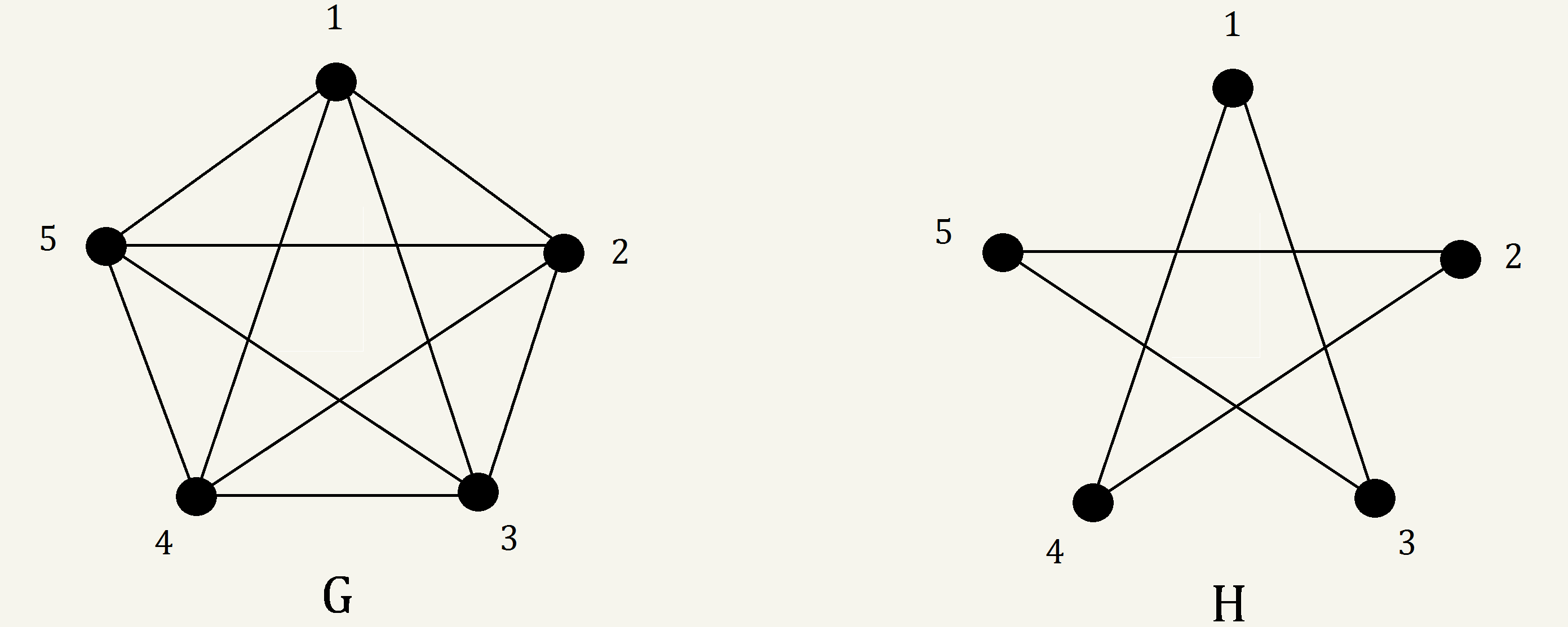
def's

$H$ is

a proper subgraph of $G$ if $V(H) \subset V(G)$ and/or $E(H) \subset E(G)$
a spanning subgraph of $G$ if $V(H) = V(G)$ and $E(H) \subseteq E(G)$
an (vertex) induced subgraph of $G$ if $H \subseteq G$ and for any pair of vertices $(x,y)$ of $G$, if both $x$ and $y$ are in $H$, then all of the edges connecting $x$ and $y$ in $G$ are also in $H$.

def's

If graph $G$ is such that for any two vertices $x$ and $y$, one can find a path from $x$ to $y$, then $G$ is connected. If $G$ isn't connected, let $k$ be the smallest integer so that $G$ can be obtained as a union of $k$ connected (sub)graphs. Then, $G$ has $k$ connected components.

def's

The distance between two vertices $v_1, v_2$ in a graph is the length of the shortest path between them. This path is the geodesic between $v_1$ and $v_2$.

def

A path graph is a graph whose vertices can be listed in the order $v_1, v_2,..., v_n$ such that all its edges are in the form $v_iv_{i+1}$ where $i=1,..., n-1$.

def

A cycle graph (or simply cycle) is a graph that consists of a single cycle. The length of a cycle graph is the number of its vertices or edges, and a cycle graph of length $n$ is denoted as $C_n$.

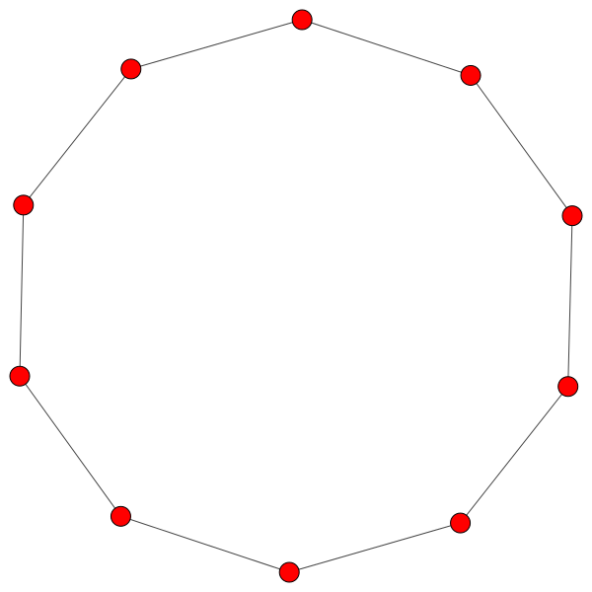
def

A complete graph is a simple undirected graph in which every distinct pair of vertices is connected by an edge. A complete graph on $n$ vertices is denoted as $K_n$.

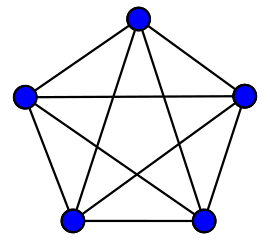
def

The complement of a graph $G$, denoted as $\bar G$, is a graph that has the same vertex set as $G$ and for all pairs of distinct vertices $u$, $v$ in $G$, $uv$ is an edge of $\bar G$ if and only if $uv$ is not an edge of $G$.

def's

A graph $G$ is regular if and only if each vertex has the same degree. A graph $G$ is irregular if and only if all of its vertices have distinct degrees.

Question: Can a simple graph be irregular?

The animation below is interactive: left-click to create a vertex; drag from a vertex to another vertex to create an edge; right-click to delete.

def

The hypercube graph on $n$ vertices (denotes as $Q_n$) is the graph formed by the vertices and edges of an $n$-dimensional hypercube. In particular, $Q_n$ has $2^n$ vertices and $n2^{n-1}$ edges.

def

Let $G$ be a graph on $n$ vertices. Then, $d_1d_2...d_n$ is a degree sequence of $G$ if and only if the vertices of $G$ can be labeled as $v_1, v_2,..., v_n$ such that $deg(v_i)=d_i$ for all $i=1, 2,..., n$.

Conventionally, $d_i \geq d_{i+1}$ for $i=1, 2,..., n-1$.

def

Graphs $G$ and $H$ are isomorphic if there is a one-to-one correspondence between the vertices of $G$ and the vertices of $H$ such that the number of edges between any pair of vertices in $G$ is equal to that between their corresponding vertices in $H$.

More formally, $G$ and $H$ are isomorphic if there is a bijection $f \colon V(G) \longrightarrow V(H)$ such that the number of edges between any vertices $X$ and $Y$ in $G$ is equal to that between $f(X)$ and $f(Y)$ in $H$.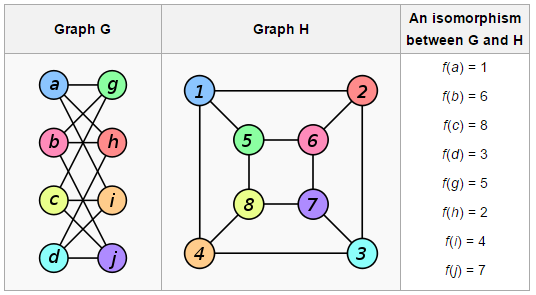

def

An automorphism of a graph $G$ is an isomorphism between $G$ and itself.

def

A graph in which each edge is assigned a direction is a directed graph or digraph.

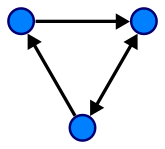
def

A digraph $G$ is strongly connected if for all vertices $a$ and $b$ in $G$, there is a path from $a$ to $b$ and vice versa.

def's

The indegree of a vertex in a digraph is the number of edges ending in that vertex. The outdegree is the number of edges starting in that vertex.

def

A digraph is balanced if the indegree is equal to the outdegree for each vertex.

def

If each edge of a complete graph is assigned with a direction, the resulting digraph is called a tournament.

def

A tournament $T$ is transitive if the fact that $ij, jk \in E(T)$ implies $ik \in E(T)$.

$$\text{Schur-Horn theorem}$$

$$\text{Let}$$ $$\{d_i\}, \{\lambda_i\}, i \in \{1,..., n\}$$ $$\text{be two sequences of reals, arranged in a non-increasing order.}$$ $$\text{Then, there is a Hermitian matrix with diagonal entries}$$ $$\{d_i\}$$ $$\text{and eigenvalues}$$ $$\{\lambda_i\}$$ $$\text{if and only if}$$ $$\sum_{i=1}^k d_i \leq \sum_{i=1}^k {\lambda_i}, \forall k \in \{1,..., n-1\}$$ $$\text{and}$$ $$\sum_{i=1}^n d_i = \sum_{i=1}^n {\lambda_i}.$$

Last updated: 7/11/2023