Recommendation: refer to the glossary along the way to help with understanding the content. Feel free to take a piece of scratch paper with you and try out some of the proofs yourself.
Let's first tackle the classic Königsberg bridges problem.
- Theorem 1.
Proof First we prove the "only if" (\(\Rightarrow\)) part. That is, the presence of a closed Eulerian trail implies that all vertices have even degrees.
Take a closed Eulerian trail (call it \(W\)) and let \(A\) be a vertex that's neither the starting nor ending point of \(W\). Assume that \(A\) is visited \(a\) times by \(W\). Because each time the trail enters \(A\) it has to exit, there are \(2a\) edges in connection with \(A\), and since the Eulerian trail uses every edge in the graph, \(A\) has a degree of \(2a\), which is even. Now, if \(B\) is denoted as the start (equivalently the end) of the trail and visited exactly \(b\) times between the start and finish, the degree of \(B\) would be \(2b+2\). So indeed every vertex has an even degree.
To prove the "if" (\(\Leftarrow\)) direction, assume that very vertex has an even degree. Take any vertex \(S\), and start walking along on an edge \(e_1\) into \(A_1\), and walk along any new edge \(e_2\) from \(A_1\), where \(A_1\) is any vertex adjacent to \(S\). Repeat this process, until a closed trail \(C_1\) is formed. Note that since \(G\) is finite (an universal assumption throughout unless specified otherwise), this \(C_1\) always exists. If \(C_1=G\), we are done; else, choose a vertex \(V_0\) in \(C_1\) such that \(C_1\) doesn't contain all edges incident at \(V_0\).
Remark: such a vertex always exists: as \(C_1 \ne G\), \(C_1\) has fewer edges than \(G\), so there is some vertex \(A\) that's not in it. However, because \(G\) is connected, there is a path from \(A\) to a vertex of \(C_1\), say it's \(V_0\). So start walking on this path, and the moment you reach \(V_0\), the most recent edge is not in \(C_1\).
Let's remove all edges of \(C_1\) from \(G\), and we obtain a graph with all even degrees again (because at the beginning all degrees are even, and by removing a closed trail, we have removed an even number of edges on each vertex). Now, starting at \(V_0\), we take another closed trail (call it \(C_2\)) in what's left. Thereafter, we can unite \(C_1\) and \(C_2\) by first walking through \(C_1\), stopping at \(V_0\), and then completing \(C_2\), coming back to \(V_0\), and finishing the rest of \(C_1\). If \(C_1 \cup C_2 = G\), we are done. Else, repeat the process above and it will eventually stop due to \(G\)'s finiteness, meaning a closed Eulerian trail has been formed on \(G\). \(\Box\)
So what can we say about the bridges now...?
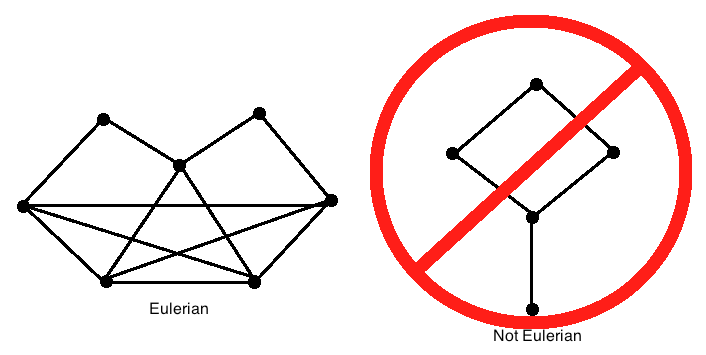
We will look at another result pertinent to the problem of bridges.
- Theorem 2
Proof Add a new edge joining \(S\) and \(T\) and call the new graph \(H\).
Claim: \(H\) has a closed Eulerian trail \(\Leftrightarrow\) \(G\) has an Eulerian trail starting at \(S\) and ending at \(T\).
Proof of the claim: left as an exercise for the readers. \( \blacksquare \)
The theorem then follows from Theorem 1 (as now in \(H\) \(deg(S)\) and \(deg(T)\) are even). \(\Box\)
With these two theorems at hand, the Königsberg bridge problem can now be tackled with ease. Try it out yourself!
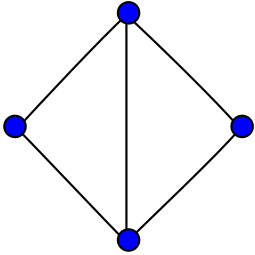
The following theorem illustrates a fundamental result that's useful in many other elementary scenarios.
- Theorem 3
Proof Take such a graph with \(e\) edges. Let \(d_1, d_2,..., d_n\) be the degrees of the \(n\) vertices of \(G\). Let's introduce a lemma.
Lemma (the Handshaking Lemma) \(\sum_{i=1}^n d_i = 2e\).
Proof of the lemma: on the left hand side, each edge is counted twice (each time by one of its two endpoints). \( \blacksquare \)
Knowing this lemma, if \(G\) has an odd number of vertices with odd degrees, the sum of degrees would also be odd but it's equal to \(2e\). \(\Box\)

Imagine the following: your year group is holding an end-of-year party and there will be a round-table dinner. Everyone will sit somewhere around a single table. Is it possible that all participants have their friends sitting next to them?
- Theorem 4 (Dirac)
Proof First note that \(G\) must be connected since otherwise, it would have a component of less than \(n/2\) vertices, meaning the vertices in that component have degrees smaller than \(n/2\).
Assume that \(G\) doesn't have a Hamiltonian cycle. Let's add new edges to \(G\) (anywhere connecting two vertices such that \(G\) remains simple) as long as we can without creating a Hamiltonian cycle. When we stop adding, we have a new graph, call it \(G'\). All vertices in \(G'\) have similarly degrees at least \(n/2\) and there's no Hamiltonian cycle. To reiterate, adding any new edge at this stage would induce a Hamiltonian cycle.
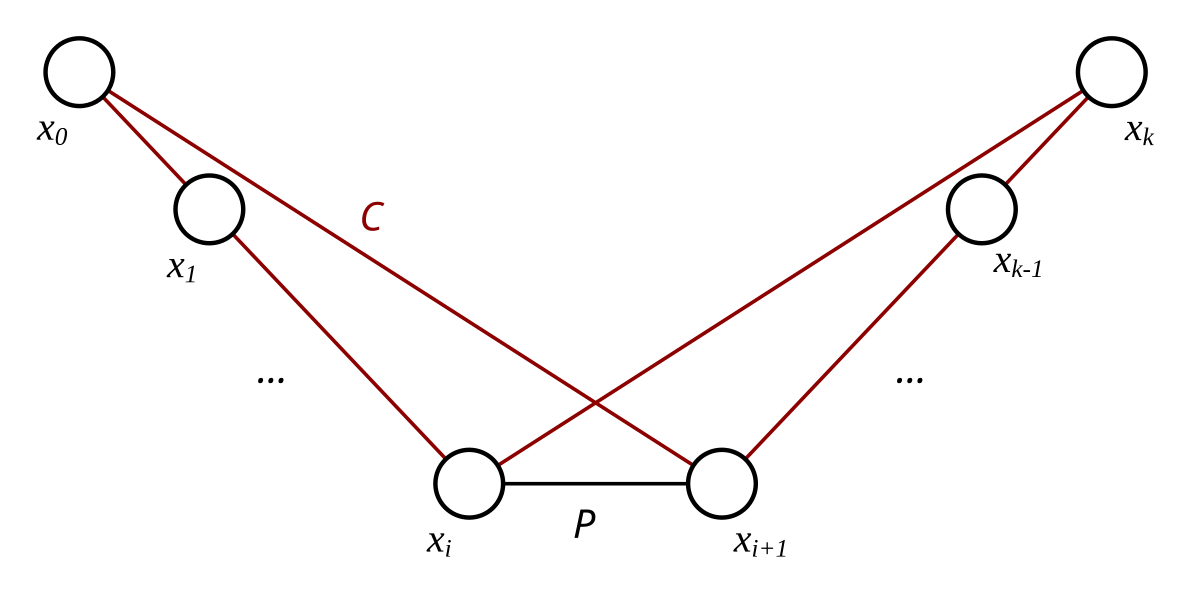
Let \(P\) be a path of maximum length in \(G'\). It's true that \(P\) contains all vertices of \(G'\): indeed, let \(x\) and \(y\) be vertices in \(G'\) such that \(xy\) is not an edge of \(G'\). As adding the edge \(xy\) would induce a Hamiltonian cycle, it follows that \(G'\) has a Hamiltonian path (encompassing all vertices) from \(x\) to \(y\). Moreover, by our initial assumption, \(deg(x)+deg(y) \geq n\).
Claim: there exists some \(i\) where \(2 \leq i \leq n-1\) such that both \(xz_i\) and \(z_{i-1}y\) are edges of \(G'\). Here, \(z_i\) denotes the \(i\)-th vertex encountered on the Hamiltonian path between \(x\) and \(y\).
Proof of the claim: Assume otherwise. Then, if \(y\) has \(k\) neighbors, \(x\) has at most \(n-(k+1)\) neighbors (\(x\) can not have any neighbor whose index is one bigger than a neighbor of \(y\), so that eliminates \(k\) choices. The "+1" denotes \(x\) neighboring with itself). Thus, \(deg(x)+deg(y) \leq n-1\). Contradiction. \( \blacksquare \)
Now, the sequence \(xz_2...z_{i-1}yz_{n-1}...z_ix\) is a Hamiltonian cycle. Contradiction. \(\Box\)
The following image illustrates the main idea of the proof (different labels).
You can interact with the following embedment: attempt to create a Hamiltonian cycle by clicking on the vertices one by one. Note: it isn't a visualization of Theorem 4, but rather a highlight of the logic that if \(G\) is Hamiltonian, it's not necessarily true that all vertices of \(G\) are of degree at least \(|G|/2 \). That is, the degree condition is sufficient for a Hamiltonian cycle to exist, but not necessary.
Notice that everything we have covered so far is related to graphs in which edges have no directions, just like two-way streets. Now, we are going to add directions to every edge, meaning we can only travel along a designated direction if we want to use it in a walk.
- Theorem 5
Proof First let's prove the conditions are necessary (\(\Rightarrow\)): as a closed Eulerian trail leaves and enters each vertex the same amount of times, \(G\) must be balanced (by definition). Meanwhile, such a trail provides a trail (path) from any vertex to any other vertex, so \(G\) must be strongly connected.
Now let's prove the conditions are sufficient (\(\Leftarrow\)). This would resemble the proof of Theorem 1. In fact, all we need to do is to replace "edges" by "directed edges" (left as an exercise for the readers). \(\Box\)
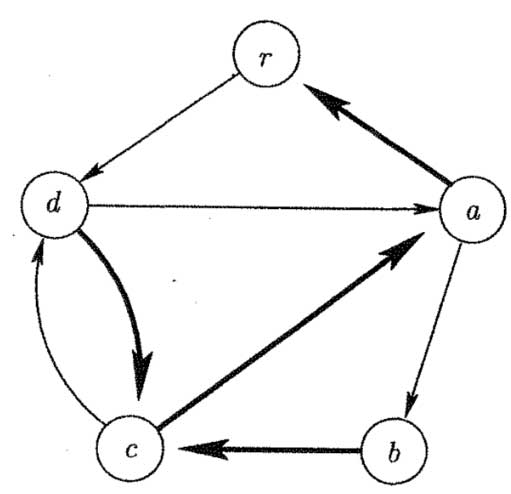
Now we will prove something similar to Theorem 4, but for directed graphs as well.
- Theorem 6
Proof First we prove the "\(\Rightarrow\)" direction (the trivial one). Indeed, if there's a Hamiltonian cycle, that cycle would provide a directed path from any vertex to any other vertex (by omitting the last edge in a cycle, we have a path). So \(T\) is strongly connected.
Now for the "\(\Leftarrow\)" direction (the non-trivial one):
Claim: \(T\) contains a cycle (not necessarily Hamiltonian).
Proof of the claim: Assume \(T\) doesn't. Then, for \(xy, yz \in E(T)\), we must have \(xz \in E(T)\) because otherwise there would be a cycle of length 3. So \(T\) is transitive, in which the vertices can be listed from left to right such that \(ij \in E(T)\) if and only if \(j\) is on the right of \(i\). But such a \(T\) isn't strongly connected as no path goes from right to left. Contradiction. \( \blacksquare \)
Now let \(C=y_1y_2...y_ky_1\) be a cycle of maximal length in \(T\), and assume \(C\) isn't Hamiltonian. As \(T\) is strongly connected and \(C\) doesn't contain all of \(V(T)\), there exists an edge from \(C\) to some vertex \(x \notin C\). Say this edge is \(y_1x\). Note that if \(xy_2\) were an edge, \(y_1xy_2...y_ky_1\) would be a cycle longer than \(C\), contradicting \(C\)'s maximality. Therefore, using the same logic, \(y_2x, y_3x,..., y_kx \in E(T)\).
Let \(Z\) be the set of vertices \(z \in V(T)\) such that \(y_1z \in E(T)\). Note that \(Z\) is neither empty nor the whole \(V(T)\), as \(x \in Z\) while \(y_1, y_k \notin Z\).
By the observation above, \(\forall z \in Z, i \in \{1,..., k\}\), we must have \(y_iz \in E(T)\) for the sake of not contradicting \(C\)'s maximality. Let \(zt\) be an edge with \(z \in Z\) and \(t \notin Z\) (such an edge exists because of the strong connectivity. More specifically, if there is no such edge, then the outdegree of \(z\) would be 0, meaning \(z\) can't get to any other vertex (you may think of it as the whole set \(Z\) having negative divergence), contradicting the strong connectivity). Also again to not contradict \(C\)'s maximality, \(t \notin C\).
Hence, \(t \notin C \cup Z\), which implies from the strong connectivity that \(ty_1 \in E(T)\) (if \(y_1t\) were instead an edge, \(t\) would be in \(Z\)), and subsequently the existence of a new cycle that's longer than \(C\): \(zty_1y_2...y_kz\). Contradiction. \(\Box\)